Gimanastyka umysłu.
Moderatorzy: gsmok, tszczesn, Romekd
- szalony
- moderator
- Posty: 1863
- Rejestracja: wt, 14 sierpnia 2007, 14:15
- Lokalizacja: Kraków/Zielona Góra
Re: Gimanastyka umysłu.
(X^X) *lnX + X^X ?
Senza mai stancià nè mai rifiatà
Cumbattenti d'onore di Santa Libertà
Parechji sò spariti à o fior' di l'età
Surghjent'è acque linde di lu fium'unità
Cumbattenti d'onore di Santa Libertà
Parechji sò spariti à o fior' di l'età
Surghjent'è acque linde di lu fium'unità
- TooL46_2
- 1875...2499 postów

- Posty: 2024
- Rejestracja: ndz, 20 lipca 2008, 12:06
- Lokalizacja: Seattle, WA
Re: Gimanastyka umysłu.
Odp na pierwsze zadanko to dy/dx = x^(x^2)[2x lnx + x]?
Pozdr,
-Tomek Drabas
________
"One should not pursue goals that are easily achieved. One must develop an instinct for what one can just barely achieve through one's greatest efforts."
—Albert Einstein
tomdrabas.com
-Tomek Drabas
________
"One should not pursue goals that are easily achieved. One must develop an instinct for what one can just barely achieve through one's greatest efforts."
—Albert Einstein
tomdrabas.com
- TooL46_2
- 1875...2499 postów

- Posty: 2024
- Rejestracja: ndz, 20 lipca 2008, 12:06
- Lokalizacja: Seattle, WA
Re: Gimanastyka umysłu.
Mamy y = x^(x^2). Logarytmujemy obie strony, czyli dostajemy lny = x^2 lnx
Teraz wyciagamy pochodna wzgledem x. Po lewej stronie uzywamy chain rule (jak to jest po polsku???), w sensie d/dy * dy/dx (lny). Po prawej stronie uzywamy product rule (znow...), czyli [f(x)*g(x)]' = f'(x)g(x)+f(x)g'(x). Dostajemy dy/dx*1/y = 2x lnx + x^2 *1/x, gdzie y = x^(x^2). Mnozymy obie strony przez y, czyli dostajemy dy/dx = x^(x^2) [2x lnx + x] Rozwiazane
Rozwiazane 
Teraz wyciagamy pochodna wzgledem x. Po lewej stronie uzywamy chain rule (jak to jest po polsku???), w sensie d/dy * dy/dx (lny). Po prawej stronie uzywamy product rule (znow...), czyli [f(x)*g(x)]' = f'(x)g(x)+f(x)g'(x). Dostajemy dy/dx*1/y = 2x lnx + x^2 *1/x, gdzie y = x^(x^2). Mnozymy obie strony przez y, czyli dostajemy dy/dx = x^(x^2) [2x lnx + x]
Pozdr,
-Tomek Drabas
________
"One should not pursue goals that are easily achieved. One must develop an instinct for what one can just barely achieve through one's greatest efforts."
—Albert Einstein
tomdrabas.com
-Tomek Drabas
________
"One should not pursue goals that are easily achieved. One must develop an instinct for what one can just barely achieve through one's greatest efforts."
—Albert Einstein
tomdrabas.com
-
OTLamp
Re: Gimanastyka umysłu.
Eee, można prościej. Wyrażenie x^(x^2) ma jak widać również zmienną w wykładniku, dlatego należy je przekształcić, aby zmienna była np. tylko w wykładniku. W tym celu można skorzystać z takiej tożsamości:
k = e^ln k
A więc analogicznie:
x^(x^2)= e^ln[x^(x^2)]
Następnie korzysta się własności logarytmu (skorzystałeś z niej od razu logarytmując u siebie obie strony równania):
ln(x^a) = a*lnx
a więc otrzymuje się:
ln[x^(x^2)] = x^2*lnx
Mamy więc ostatecznie:
d/dx x^(x^2) = d/dx e^(x^2*lnx)
i to już liczy się jako pochodną normalnej funkcji złożonej.
k = e^ln k
A więc analogicznie:
x^(x^2)= e^ln[x^(x^2)]
Następnie korzysta się własności logarytmu (skorzystałeś z niej od razu logarytmując u siebie obie strony równania):
ln(x^a) = a*lnx
a więc otrzymuje się:
ln[x^(x^2)] = x^2*lnx
Mamy więc ostatecznie:
d/dx x^(x^2) = d/dx e^(x^2*lnx)
i to już liczy się jako pochodną normalnej funkcji złożonej.
-
OTLamp
Re: Gimanastyka umysłu.
Wykazać, że wyrażenie z załącznika jest liczbą całkowitą i ją podać 
- Załączniki
-
- wyrażenie.GIF (3.45 KiB) Przejrzano 320 razy
- Thereminator
- 6250...9374 posty
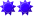
- Posty: 7359
- Rejestracja: sob, 2 kwietnia 2005, 21:42
- Lokalizacja: Nizina Wschodnioeuropejska
Re: Gimanastyka umysłu.
Na moją głupią zagadkę z poprzedniej strony (o której sam już zapomniałem) nikt nie odpowiedział, więc sam odpowiem - cegła 
W teorii nie ma różnicy między praktyką a teorią. W praktyce jest.
- TooL46_2
- 1875...2499 postów

- Posty: 2024
- Rejestracja: ndz, 20 lipca 2008, 12:06
- Lokalizacja: Seattle, WA
Re: Gimanastyka umysłu.
Wyszlo mi cos takiego, jak w zalacznikuOTLamp pisze:Wykazać, że wyrażenie z załącznika jest liczbą całkowitą i ją podać
- Załączniki
-
- SolutionForum.pdf
- (30.23 KiB) Pobrany 74 razy
Pozdr,
-Tomek Drabas
________
"One should not pursue goals that are easily achieved. One must develop an instinct for what one can just barely achieve through one's greatest efforts."
—Albert Einstein
tomdrabas.com
-Tomek Drabas
________
"One should not pursue goals that are easily achieved. One must develop an instinct for what one can just barely achieve through one's greatest efforts."
—Albert Einstein
tomdrabas.com
-
OTLamp
Re: Gimanastyka umysłu.
No wyszło dobrze, ale trzeba przyznać, że jesteś niekwestionowanym mistrzem komplikowania prostych rzeczy  Analizując y, wystarczy zauważyć, że (2+sqrt5)(2-sqrt5)=-1. Wtedy od razu dostajesz y=-x. W zasadzie podczas normalnego liczenia to wychodzi samo po wymnożeniu pierwiastków, bez stosowania dodatkowych zmiennych (y). Można z tego zadania zrobić straszak dla jakichś maturzystów, wiedząc że ww. wyrażenie jest równe 1, można w zapisie tego wyrażenia dwójki zapisać np. jako 1+wyrażenie. Wtedy całe zadanie będzie miało odstraszającą postać, ale będzie banalne do rozwiązania.
Analizując y, wystarczy zauważyć, że (2+sqrt5)(2-sqrt5)=-1. Wtedy od razu dostajesz y=-x. W zasadzie podczas normalnego liczenia to wychodzi samo po wymnożeniu pierwiastków, bez stosowania dodatkowych zmiennych (y). Można z tego zadania zrobić straszak dla jakichś maturzystów, wiedząc że ww. wyrażenie jest równe 1, można w zapisie tego wyrażenia dwójki zapisać np. jako 1+wyrażenie. Wtedy całe zadanie będzie miało odstraszającą postać, ale będzie banalne do rozwiązania.
- TooL46_2
- 1875...2499 postów

- Posty: 2024
- Rejestracja: ndz, 20 lipca 2008, 12:06
- Lokalizacja: Seattle, WA
Re: Gimanastyka umysłu.
RacjaOTLamp pisze:Analizując y, wystarczy zauważyć, że (2+sqrt5)(2-sqrt5)=-1.
Pozdr,
-Tomek Drabas
________
"One should not pursue goals that are easily achieved. One must develop an instinct for what one can just barely achieve through one's greatest efforts."
—Albert Einstein
tomdrabas.com
-Tomek Drabas
________
"One should not pursue goals that are easily achieved. One must develop an instinct for what one can just barely achieve through one's greatest efforts."
—Albert Einstein
tomdrabas.com
- Tomasz Gumny
- 1875...2499 postów

- Posty: 2301
- Rejestracja: pn, 1 stycznia 2007, 23:18
- Lokalizacja: Trzcianka/Poznań
- Kontakt:
Re: Gimanastyka umysłu.
Zadanie domowe syna:
Usunąć niewymierność z mianownika:

Jakieś pomysły? Ja się poddałem.
Usunąć niewymierność z mianownika:
Jakieś pomysły? Ja się poddałem.
- Załączniki
-
- niewym.png (1.4 KiB) Przejrzano 320 razy
Tomek
Re: Gimanastyka umysłu.
Na jutro?
I w jakiej szkole (podstawowa/gim/średnia) jest syn?
I w jakiej szkole (podstawowa/gim/średnia) jest syn?
http://www.pajacyk.pl/index.php
--
Wszelkie pytania o proszę kierować na kacper@selenoid.pl
--
Pozdrawiam, Kacper
--
Wszelkie pytania o proszę kierować na kacper@selenoid.pl
--
Pozdrawiam, Kacper
-
OTLamp
Re: Gimanastyka umysłu.
Z prawą częścią nie ma problemu, wystarczy licznik i mianownik wymnożyć przez pierwiastek trzeciego stopnia z 6^2, w wyniku czego otrzymuje się (wspomniany pierwiastek)/2.Tomasz Gumny pisze:Zadanie domowe syna:
Usunąć niewymierność z mianownika:
Jakieś pomysły? Ja się poddałem.
Mianownik lewej części można "załatwić" korzystając ze wzoru skróconego mnożenia na sumę sześcianów:
x^3+y^3= (x+y)(x^2-xy+y2)
z tego wynika, że:
x+y=(x^3+y^3)/(x^2-xy+y2)
a z kolei z tego wynika, że
1/(x+y)=(x^2-xy+y2)/(x^3+y^3)
x to nasz pierwiastek trzeciego stopnia z 6, a y to ten pierwiastek z 4. Po podstawieniu mamy w mianowniku (6+4).